• C++

  • 十大经典排序算法

  • @ 2026-1-24 11:20:24

原文链接

本系列算法整理自：https://github.com/hustcc/JS-Sorting-Algorithm

同时也参考了维基百科做了一些补充。

排序算法是《数据结构与算法》中最基本的算法之一。

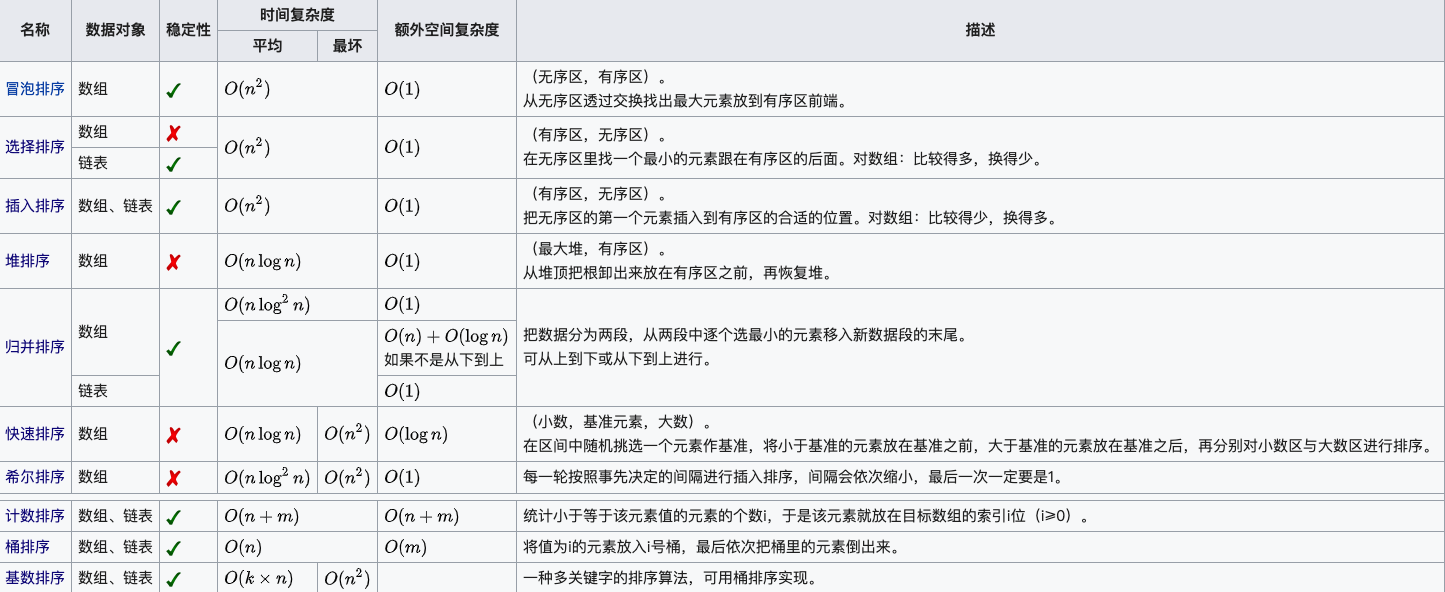
排序算法可以分为内部排序和外部排序，内部排序是数据记录在内存中进行排序，而外部排序是因排序的数据很大，一次不能容纳全部的排序记录，在排序过程中需要访问外存。常见的内部排序算法有：插入排序、希尔排序、选择排序、冒泡排序、归并排序、快速排序、堆排序、基数排序等。用一张图概括：

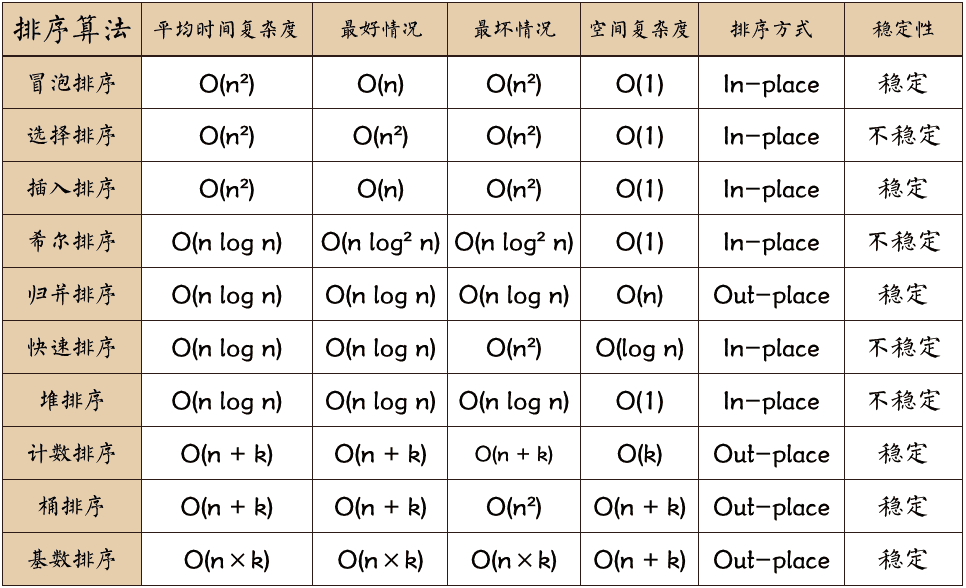
点击以下图片查看大图：

关于时间复杂度

平方阶 (O(n2)) 排序 各类简单排序：直接插入、直接选择和冒泡排序。

线性对数阶 (O(nlog2n)) 排序 快速排序、堆排序和归并排序；

O(n1+§)) 排序，§ 是介于 0 和 1 之间的常数。 希尔排序

线性阶 (O(n)) 排序 基数排序，此外还有桶、箱排序。

关于稳定性

稳定的排序算法：冒泡排序、插入排序、归并排序和基数排序。

不是稳定的排序算法：选择排序、快速排序、希尔排序、堆排序。

名词解释：

  • n：数据规模
  • k："桶"的个数
  • In-place：占用常数内存，不占用额外内存
  • Out-place：占用额外内存
  • 稳定性：排序后 2 个相等键值的顺序和排序之前它们的顺序相同

包含以下内容：

相关书籍

双向冒泡排序

双向冒泡排序，又叫鸡尾酒排序（Cocktail Sort）。

它的过程是：先从左往右比较一次，再从右往左比较一次，然后又从左往右比较一次，以此类推。

它是为了优化前面的大部分元素都已经排好序的数组的排序，例如对于数组 [2,3,4,5,6,7,8,1]，如果使用普通的冒泡排序，需要比较七次；而换成双向冒泡排序，只需比较三次。

public void cocktailSort(int[] a) {
    int left = 0;
    int right = a.length - 1;

    while (left < right) {
        for (int i = left; i < right; i++) { // 保证 a[right] 是最大的
            if (a[i] > a[i+1]) {
                swap(a, i, i+1);
            }
        }
        right--;
        for (int i = right; i > left; i--) { // 保证 a[left] 是最小的
            if (a[i] < a[i-1]) {
                swap(a, i, i-1);
            }
        }
        left++;
    }
}

归并排序C++容易理解版本

#include <iostream>
#include <vector>
using namespace std;

// 合并两个有序子数组
void merge(vector<int>& arr, int left, int mid, int right) {
    vector<int> temp(right - left + 1);
    int i = left, j = mid + 1, k = 0;
    
    // 合并两个有序子数组[4](@ref)
    while (i <= mid && j <= right) {
        if (arr[i] <= arr[j]) {
            temp[k++] = arr[i++];
        } else {
            temp[k++] = arr[j++];
        }
    }
    
    // 复制剩余元素[3](@ref)
    while (i <= mid) {
        temp[k++] = arr[i++];
    }
    
    while (j <= right) {
        temp[k++] = arr[j++];
    }
    
    // 将临时数组复制回原数组[1](@ref)
    for (int idx = 0; idx < k; idx++) {
        arr[left + idx] = temp[idx];
    }
}

// 归并排序（原地修改）
void merge_sort_inplace(vector<int>& arr, int left, int right) {
    if (left < right) {
        int mid = left + (right - left) / 2;
        
        // 递归排序左右子数组[6](@ref)
        merge_sort_inplace(arr, left, mid);
        merge_sort_inplace(arr, mid + 1, right);
        
        // 合并已排序的子数组[4](@ref)
        merge(arr, left, mid, right);
    }
}

// 包装函数，简化调用
void merge_sort(vector<int>& arr) {
    if (!arr.empty()) {
        merge_sort_inplace(arr, 0, arr.size() - 1);
    }
}

int main() {
    vector<int> arr = {38, 27, 43, 3, 9, 82, 10};
    
    cout << "原始数组: ";
    for (int num : arr) {
        cout << num << " ";
    }
    cout << endl;
    
    merge_sort(arr);
    
    cout << "排序后数组: ";
    for (int num : arr) {
        cout << num << " ";
    }
    cout << endl;
    
    return 0;
}

//迭代版本 
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;

// 合并两个有序子数组
void merge(vector<int>& arr, int left, int mid, int right, vector<int>& temp) {
    int i = left, j = mid + 1, k = left;
    
    // 合并两个有序子数组[1,4](@ref)
    while (i <= mid && j <= right) {
        if (arr[i] <= arr[j]) {
            temp[k++] = arr[i++];
        } else {
            temp[k++] = arr[j++];
        }
    }
    
    // 复制剩余元素[1,4](@ref)
    while (i <= mid) {
        temp[k++] = arr[i++];
    }
    
    while (j <= right) {
        temp[k++] = arr[j++];
    }
    
    // 将临时数组复制回原数组[1](@ref)
    for (int idx = left; idx <= right; idx++) {
        arr[idx] = temp[idx];
    }
}

// 归并排序迭代版本
void merge_sort_iterative(vector<int>& arr) {
    int n = arr.size();
    if (n <= 1) return;
    
    vector<int> temp(n);
    
    // 从底部开始，逐步增加子数组大小[1,4](@ref)
    for (int width = 1; width < n; width *= 2) {
        // 每次处理两个相邻的子数组[1](@ref)
        for (int left = 0; left < n; left += 2 * width) {
            // 计算中点，注意边界保护[3](@ref)
            int mid = min(left + width - 1, n - 1);
            int right = min(left + 2 * width - 1, n - 1);
            
            // 只有当存在两个子数组需要合并时才进行合并[1](@ref)
            if (mid < right) {
                merge(arr, left, mid, right, temp);
            }
        }
    }
}

int main() {
    vector<int> arr = {38, 27, 43, 3, 9, 82, 10};
    
    cout << "原始数组: ";
    for (int num : arr) {
        cout << num << " ";
    }
    cout << endl;
    
    merge_sort_iterative(arr);
    
    cout << "排序后数组: ";
    for (int num : arr) {
        cout << num << " ";
    }
    cout << endl;
    
    // 测试更多例子
    vector<int> arr2 = {5, 2, 8, 1, 9, 3, 7, 4, 6};
    cout << "另一个测试数组: ";
    for (int num : arr2) {
        cout << num << " ";
    }
    cout << endl;
    
    merge_sort_iterative(arr2);
    
    cout << "排序后: ";
    for (int num : arr2) {
        cout << num << " ";
    }
    cout << endl;
    
    return 0;
}

第k大数递归版

#include <iostream>
#include <vector>
#include <cstdlib>
#include <ctime>
#include <algorithm>
using namespace std;

// 随机分区函数，返回大于基准值的元素个数
int partition(vector<int>& nums, int left, int right) {
    // 随机选择基准值
    int random_index = left + rand() % (right - left + 1);
    swap(nums[left], nums[random_index]);
    int pivot = nums[left];
    
    // 将大于基准值的元素移到左边，小于等于基准值的元素移到右边
    int i = left + 1, j = right;
    while (i <= j) {
        if (nums[i] >= pivot) {
            i++;
        } else if (nums[j] <= pivot) {
            j--;
        } else {
            swap(nums[i], nums[j]);
            i++;
            j--;
        }
    }
    
    // 将基准值放到正确的位置
    swap(nums[left], nums[j]);
    
    // 返回大于基准值的元素个数
    return j - left;
}

// 快速选择算法，返回第k大的数
int quickSelect(vector<int>& nums, int left, int right, int k) {
    if (left == right) return nums[left];
    
    // 进行分区
    int cnt = partition(nums, left, right);
    
    // 判断第k大的数在哪一部分
    if (k <= cnt) {
        // 在左半部分（大于基准值的部分）
        return quickSelect(nums, left, left + cnt - 1, k);
    } else if (k == cnt + 1) {
        // 基准值正好是第k大的数
        return nums[left + cnt];
    } else {
        // 在右半部分（小于等于基准值的部分）
        return quickSelect(nums, left + cnt + 1, right, k - cnt - 1);
    }
}

// 包装函数，方便调用
int findKthLargest(vector<int>& nums, int k) {
    srand(time(0)); // 初始化随机种子
    return quickSelect(nums, 0, nums.size() - 1, k);
}

int main() {
    // 测试示例
    vector<int> nums = {3, 2, 1, 5, 6, 4};
    int k = 2; // 找第2大的数
    
    cout << "数组: ";
    for (int num : nums) cout << num << " ";
    cout << endl;
    
    int result = findKthLargest(nums, k);
    cout << "第" << k << "大的数是: " << result << endl;
    
    // 验证：排序后查看
    vector<int> sorted_nums = nums;
    sort(sorted_nums.begin(), sorted_nums.end(), greater<int>());
    cout << "排序后数组（从大到小）: ";
    for (int num : sorted_nums) cout << num << " ";
    cout << endl;
    
    return 0;
}

第K大数迭代版

这个算法是快速排序思想在查找问题上的经典应用，在实际工程中非常高效，是C++标准库std::nth_element函数的实现原理。

int quickSelectIterative(vector<int>& nums, int k) {
    int left = 0, right = nums.size() - 1;
    srand(time(0));
    
    while (true) {
        if (left == right) return nums[left];
        
        // 随机分区
        int random_index = left + rand() % (right - left + 1);
        swap(nums[left], nums[random_index]);
        int pivot = nums[left];
        
        int i = left + 1, j = right;
        while (i <= j) {
            if (nums[i] >= pivot) i++;
            else if (nums[j] < pivot) j--;
            else swap(nums[i++], nums[j--]);
        }
        swap(nums[left], nums[j]);
        
        int cnt = j - left; // 大于基准值的元素个数
        
        if (k <= cnt) {
            right = j - 1;
        } else if (k == cnt + 1) {
            return nums[j];
        } else {
            left = j + 1;
            k -= (cnt + 1);
        }
    }
}

1 条评论

  • 1
146
已通过
0
题解被赞
  1. 评测队列
  2. 服务状态
  3. 兼容模式
  4. 主题
  2. 晋ICP备2025064124号
  3. Worker 0, 19ms
  4. Powered by Hydro v5.0.0-beta.17 Community, Modified by TOOTD