题目描述

小 M 最近学会了如何用线段树维护序列，并支持区间求和的操作。

以下给出本题中线段树的定义。该定义可能和你熟知的线段树有区别。

• 线段树是一种有根的二叉树，其每个节点对应了序列上的一个区间 $[l, r)$，其中根节点对应 $[0, n)$。
• 对于每个节点，若其代表的序列区间 $[l, r)$ 满足 $r - l = 1$，则其为叶节点；否则设 $m = \lfloor \frac{l + r}{2} \rfloor$，该节点左儿子代表区间 $[l, m)$，右儿子代表区间 $[m, r)$。

定义 $f(l, r)$ 表示区间 $[l, r)$ 的和最少可以用多少个节点的区间和的和表示，即在进行线段树区间查询时停止向下继续访问的节点个数。

现在给定 $n$ 和 $k$，求满足 $f(l, r) = k$ 的区间 $[l, r)$ 的个数。

输入格式

本题采用多组测试数据。

第一行输入两个正整数 $c$ ($0 \le c \le 10$), $t$，表示当前测试点的编号和数据组数。

对于每组测试数据，输入两个正整数 $n$, $k$。

输出格式

输出 $t$ 行，每行一个整数，第 $i$ 行的输出表示第 $i$ 组测试数据的答案。

样例

Input 1

0 3
3 2
10 2
147 7

Output 1

1
19
1477

数据范围

• 对于 $20\%$ 的数据，有 $n \leq 700$（测试点编号 $1, 2$）。
• 对于 $40\%$ 的数据，有 $n \leq 8 \times 10^3$（测试点编号 $1, 2, 3, 4$）。
• 对于 $60\%$ 的数据，有 $n \leq 2 \times 10^4$（测试点编号 $1, 2, 3, 4, 5, 6$）。
• 对于另外 $20\%$ 的数据，有 $k = 1$（测试点编号 $7, 8$）。
• 对于 $100\%$ 的数据，有 $t \leq 5$，$k \leq n \leq 10^9$。

本题对线段树的定义部分来自 WC2024 C题 线段树。

样例解释

$c$ 在样例中等于 $0$。

这里仅给出第一组数据的样例解释。

我们有形如下图的线段树。

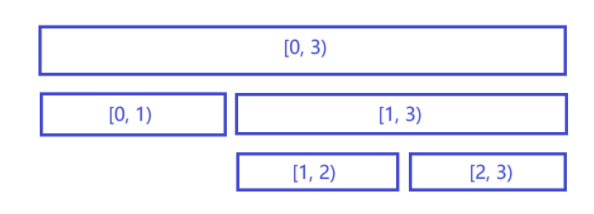
对于所有的区间：

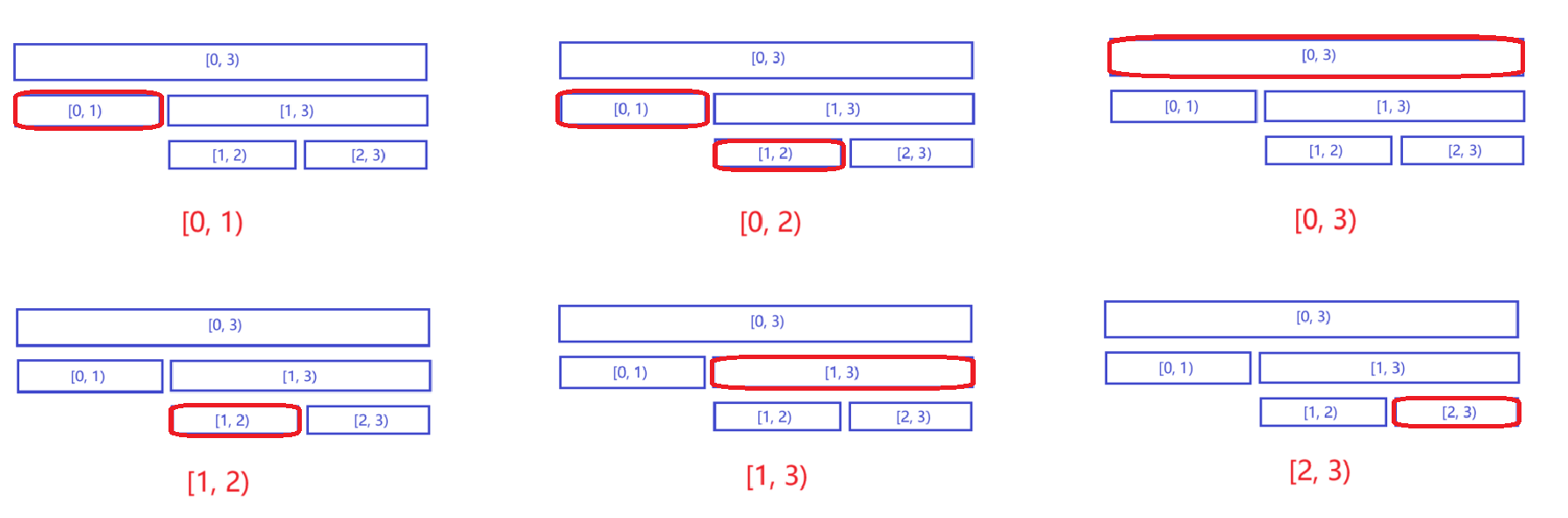
由上图可见，只有区间 [0,2)[0, 2) 选取了两个区间，故答案为 1。